2-complexes with large 2-girth

////////////////////////////////////////////

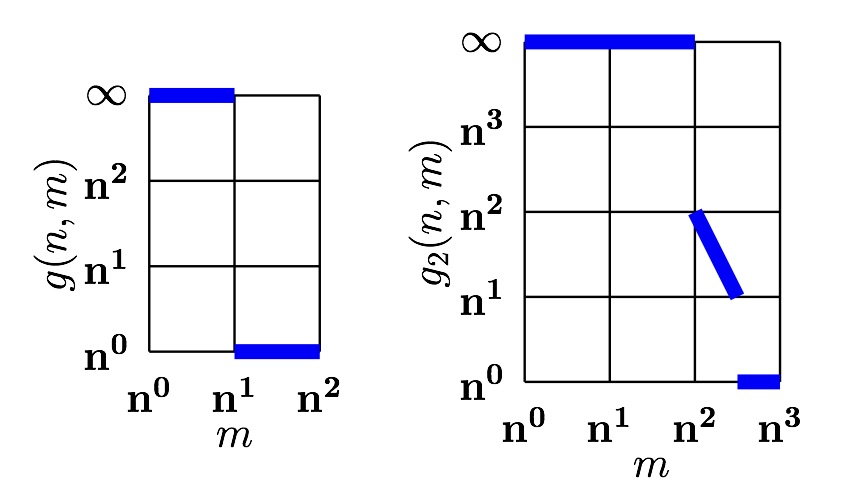
The 2-girth of a 2-dimensional simplicial complex X is the minimum size of a non-zero 2-cycle in $H_2(X,\mathbb{ℤ}/2)$. We consider the maximum possible girth of a complex with $n$ vertices and $m$ 2-faces. If $m=n^{2+\alpha}$ for $\alpha<1/2,$ then we show that the $$2-girth is at most $n^{2−2 \alpha}$ and we prove the existence of complexes with $2$-girth at least c_{\alpha, \epsilon} n^{2−2 \alpha - \epsilon}$. On the other hand, if $\alpha >1/2$, the $2$-girth is at most $C_{\alpha}$. So there is a phase transition as $\alpha$ passes $1/2$. Our results depend on a new upper bound for the number of combinatorial types of triangulated surfaces with $v$ vertices and $f$ faces.